毕业论文函数怎么写？gz数学在整个数学领域，处于一个什么水平？

毕业论文函数怎么写？

写毕业论文涉及函数时，可以根据具体的研究目的和问题来决定需要用到哪些函数。以下是一些建议：

1. 引言部分：在引言中，可以简要介绍研究领域的相关理论和已有的研究成果。根据需要，可以引用相关的函数、模型或理论，用于支撑研究的基础和理论框架。

2. 研究方法：在研究方法部分，介绍用于数据采集、分析和处理的方法和技术。这可能包括统计学方法、模型建立、实验设计等。在描述这些方法时，需要详细说明所使用的函数和算法，以及它们的目的和作用。

3. 数据分析：在数据分析部分，根据研究目标和研究问题，使用适当的函数来处理和分析研究所得到的数据。这可能涉及到统计分析、回归模型、计算模拟、图表绘制等。需要在论文中提供相关函数的名称、参数说明和应用方式，确保读者能够理解和重复实验结果。

4. 结果展示：在结果展示部分，可以使用适当的函数将数据处理结果以可视化的方式呈现出来。这可能包括表格、图表、图像等。在使用这些函数时，需要提供所用函数的名称、参数设置和结果解释。

5. 讨论和结论：在论文的讨论和结论部分，可以根据研究结果进行深入分析和解释。这可能要借助于相关的函数和模型来描述和解释实验结果，并回答研究问题。

gz数学在整个数学领域，处于一个什么水平？

作为一位gz数学老师，我来回答这个问题。

gz数学在整个数学领域，仅仅处于初级阶段，为什么这么说呢？有以下几个原因：

数学无用论

高喊数学无用论的，一般都在说gz数学。因为gz数学在gz学科中算是比较难的科目，虽然在数学界，他仅仅是初级阶段。很多人说学数学有什么用？确实，gz数学对实际生活指导作用并不大，举一个平面向量的例子，平面向量的诞生就是为了解决物理问题，物理中力有大小有方向，做功也需要方向和大小，为了解决这个问题，诞生了向量这一学科。但是实话实说，仅仅学数学的平面向量，是体会不到它的应用价值的。也是正因为gz数学太过于初级，所以才有这么多说数学无用论。事实上，任何一个学科只要研究到尖端领域，才会感觉到数学的价值。

我认为gz数学的价值，一个是高考分数，这个无可厚非，另一个是训练逻辑思维能力，但是它的效果并不可见。

数学书上已标明

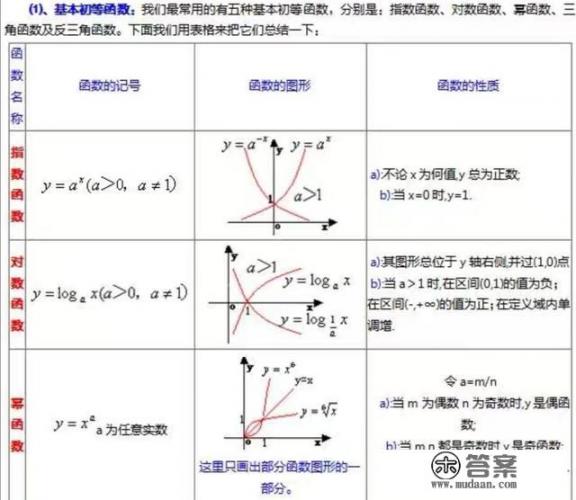
在gz必修一，讲的是整个gz的重点，就是函数。而函数中指数对数幂，这三个函数确是重点中的重点。这一节，有一个响亮的名字，叫做基本初等函数。

DX学的数学才是高等数学

有很多小朋友把gz数学简称为高数，其实非也，DX数学课程才叫高等数学，简称高数。

而作为DX高数的基础课，是微积分，换句话说，微积分是高等数学的第一课，而gz对微积分要求并不高，导数研究的还算不错，但是，积分仅仅是点到为止。通过这个层面也可以看出，gz数学确实是很基础的。

以上是我对gz数学在数学领域处于什么位置的回答，希望大家补充讨论。

自己不是数学专业的，自己感觉高数是众学科的基石基础学科，看看考研数一数二，不管什么专业必考，也是学会了高数，才能在力学个个公示中慢慢分析推导，个人学力学所以只能这么举例。

说一句比较令人丧气的话，别说gz数学了，哪怕你上DX学完了高等数学，那也连数学大门的门槛还没有迈进去呢。真正的数学追求的是公理化，抽象化与符号化，而这些特征在gz数学乃至高等数学中均不具备。可以说，gz数学甚至还只停留在算术的阶段。

由于现代数学理论过于抽象且发展是非线性的，因此很难用通俗的语言解释，我只是用大家都能理解的时间线索来大致说明一下。

gz数学的绝大多数内容都是初等数学，所谓初等数学是指不涉及极限概念或者说微积分知识的数学，gz数学即使有少部分涉及到了微积分，也是极浅的皮毛。而微积分的发明是在17世纪，那时满清也才刚刚入关而已，因此gz数学从时间线上只相当于明朝时期。

上了DX会学高等数学，但只是极其简陋的微积分，时间上也就相当于到了康熙乾隆年间，稍微深一点的知识就是傅里叶级数了，算是勉强能达到道光年间，但这已经是最深的了。这就意味着我们就算DX学完了数学，也只是摸到了点鸦片战争之前的门槛。真正的数学还太遥远太遥远

更惨的是，你在高等数学里学的那个微积分，在光绪年间就被数学界所淘汰了，取而代之的是一种被称为勒贝格积分的新型积分，而这是你在高等数学里边完全学不到的。

因此，中国大部分人的数学水平基本都停留在乾隆年间，即使是受过完整教育的DX本科生也止步于鸦片战争了。

如果你DX报考的数学系，则会接触到真正的专业的数学，那么就有希望在本科阶段看到民国的曙光。但是也仅此而已了，只有一些顶尖XX的数学系可能才会进展到国民政府时期的数学。

因此，数学是一个无底深渊，把它比喻成马里亚纳海沟的话，gz数学还只是在海岸上晃悠呢，连水都没下。因此，做数学需要极大的勇气与毅力，那些真正肯埋下头来脚踏实地的做研究的人，是值得我们敬佩的！

这个问题嘛。。。

个人DX是应数专业的，记得大二的时候数分讲师说过：“ 现在学习的数学还是基础 ”。如果这样算的话，gz数学应该就是基础中的基础了吧😂。这样说或许有些不甘心，但事实就是如此。学过DX那所谓的基础的数学过后再去观察gz数学的话，就数学这一领域来说，gz数学真的不算什么。